Изгиб кривизна 4 буквы. Изгиб (механика)
 σ z = E ε z {\displaystyle \sigma _{z}=E\varepsilon _{z}}
σ z = E ε z {\displaystyle \sigma _{z}=E\varepsilon _{z}}то есть напряжения также распределены по линейному закону.
В сечении балки (в плоском случае) возникают изгибающий момент M x {\displaystyle M_{x}}, поперечная сила Q y {\displaystyle Q_{y}} и продольная сила N {\displaystyle N}. На сечение действует внешняя распределенная нагрузка q {\displaystyle q}.
Рассмотрим два смежных сечения, расположенных на расстоянии d z {\displaystyle dz} друг от друга. В деформированном состоянии они развернуты на угол d θ {\displaystyle d\theta } друг относительно друга. Так как верхние слои растянуты, а нижние сжаты, то очевидно, что существует нейтральный слой, остающийся нерастянутым. На рисунке он выделен красным. Изменение кривизны нейтрального слоя записывается следующим образом:
1 ρ = d θ d z {\displaystyle {\frac {1}{\rho }}={\frac {d\theta }{dz}}}Приращение длины отрезка АВ, находящегося на расстоянии y {\displaystyle y} от нейтральной оси, выражается следующим образом:
Δ l = (y + ρ) d θ − ρ d θ = y d θ {\displaystyle \Delta l=(y+\rho)d\theta -\rho d\theta =yd\theta }Таким образом, деформация:
ε z = Δ l l = y d θ ρ d θ = y ρ {\displaystyle \varepsilon _{z}={\frac {\Delta l}{l}}={\frac {yd\theta }{\rho d\theta }}={\frac {y}{\rho }}}Силовые соотношения
σ z = E ε z = E y ρ {\displaystyle \sigma _{z}=E\varepsilon _{z}=E{\frac {y}{\rho }}}Свяжем напряжение с силовыми факторами, возникающими в сечении. Осевая сила выражается следующим образом:
N = ∫ A. σ z d A = ∫ A. E y ρ d A = E ρ ∫ A. y d A {\displaystyle N=\int \limits _{A}^{\color {White}.}{\sigma _{z}}\,dA=\int \limits _{A}^{\color {White}.}{E{\frac {y}{\rho }}}\,dA={\frac {E}{\rho }}\int \limits _{A}^{\color {White}.}y\,dA}Интеграл в последнем выражении представляет собой статический момент сечения относительно оси x {\displaystyle x}. Принято брать в качестве оси x {\displaystyle x} центральную ось сечения, такую, что
S x = ∫ A. y d A = 0 {\displaystyle S_{x}=\int \limits _{A}^{\color {White}.}y\,dA=0}Таким образом, N = 0 {\displaystyle N=0}. Изгибающий момент выражается следующим образом:
M x = ∫ A. σ z y d A = E ρ ∫ A. y 2 d A = E ρ J x {\displaystyle M_{x}=\int \limits _{A}^{\color {White}.}{\sigma _{z}y}\,dA={\frac {E}{\rho }}\int \limits _{A}^{\color {White}.}{y^{2}}\,dA={\frac {E}{\rho }}J_{x}}где J x = ∫ A. y 2 d A {\displaystyle J_{x}=\int \limits _{A}^{\color {White}.}{y^{2}}\,dA} - момент инерции сечения относительно оси x {\displaystyle x}.
Напряжения в сечении могут также приводиться к моменту M y {\displaystyle M_{y}}. Чтобы этого не произошло, необходимо выполнение условия:
M y = E ρ ∫ A. y x d A = E ρ J x y = 0 {\displaystyle M_{y}={\frac {E}{\rho }}\int \limits _{A}^{\color {White}.}{yx}\,dA={\frac {E}{\rho }}J_{xy}=0}то есть центробежный момент инерции должен быть равен нулю, и ось y {\displaystyle y} должна быть одной из главных осей сечения.
Таким образом, кривизна изогнутой оси балки связана с изгибающим моментом выражением:
1 ρ = M x E J x {\displaystyle {\frac {1}{\rho }}={\frac {M_{x}}{EJ_{x}}}}Распределение напряжений по высоте сечения выражается формулой:
σ = M x J x y {\displaystyle \sigma ={\frac {M_{x}}{J_{x}}}y}Максимальное напряжение в сечении выражается формулой:
σ m a x = M x J x h 2 = M x W x {\displaystyle \sigma _{max}={\frac {M_{x}}{J_{x}}}{\frac {h}{2}}={\frac {M_{x}}{W_{x}}}}где W x = J x h 2 {\displaystyle W_{x}={\frac {J_{x}}{\frac {h}{2}}}} - момент сопротивления сечения изгибу, h {\displaystyle h} - высота сечения балки.
Величины J x {\displaystyle J_{x}} и W x {\displaystyle W_{x}} для простых сечений (круглое, прямоугольное) вычисляются аналитически. Для круглого сечения диаметром d {\displaystyle d}:
J x = π d 4 64 {\displaystyle J_{x}={\frac {\pi d^{4}}{64}}}
W x = π d 3 32 {\displaystyle W_{x}={\frac {\pi d^{3}}{32}}}
Для прямоугольного сечения высотой h {\displaystyle h} и шириной b {\displaystyle b}
J x = b h 3 12 {\displaystyle J_{x}={\frac {bh^{3}}{12}}}
W x = b h 2 6 {\displaystyle W_{x}={\frac {bh^{2}}{6}}}
Для более сложных сечений (например, швеллер, двутавр), имеющих стандартизованные размеры, эти величины приведены в справочной литературе.
Изгибающий момент в сечении может быть получен методом сечений (если балка статически определима) или методами сил/перемещений.
Дифференциальные уравнения равновесия. Определение перемещений
Основными перемещениями, возникающими при изгибе, являются прогибы v {\displaystyle v} в направлении оси y {\displaystyle y}. Необходимо связать их с изгибающим моментом в сечении. Запишем точное соотношение, связывающее прогибы и кривизну изогнутой оси:
1 ρ = v ″ (1 + v ′ 2) 3 2 {\displaystyle {\frac {1}{\rho }}={\frac {v""}{(1+v"^{2})^{\frac {3}{2}}}}}Так как прогибы и углы поворота предполагаются малыми, то величина
v ′ 2 = (t g (θ)) 2 ≈ θ 2 {\displaystyle v"^{2}=\left(\mathrm {tg} \,(\theta)\right)^{2}\approx \theta ^{2}}является малой. Следовательно,
1 ρ ≈ v ″ {\displaystyle {\frac {1}{\rho }}\approx v""}Запишем уравнение равновесия сечения в направлении оси y {\displaystyle y}:
Q y + q d z − Q y − d Q y = 0 ⇛ d Q d z = q {\displaystyle Q_{y}+qdz-Q_{y}-dQ_{y}=0\Rrightarrow {\frac {dQ}{dz}}=q}Запишем уравнение равновесия моментов относительно оси x {\displaystyle x}:
M x + Q d z + q d z d z 2 − M x − d M x = 0 {\displaystyle M_{x}+Q\,dz+q\,dz{\frac {\,dz}{2}}-M_{x}-\,dM_{x}=0}Величина q d z d z 2 {\displaystyle q\,dz{\frac {\,dz}{2}}} имеет 2-й порядок малости и может быть отброшена. Следовательно,
d M x d z = Q y {\displaystyle {\frac {\,dM_{x}}{\,dz}}=Q_{y}}Таким образом, имеется 3 дифференциальных уравнения. К ним добавляется уравнение для перемещений:
d v d z = t g θ ≈ θ {\displaystyle {\frac {\,dv}{\,dz}}=\mathrm {tg} \,\theta \approx \theta }В векторно-матричной форме система записывается следующим образом:
d Z → d z + A Z → = b → {\displaystyle {\frac {\,d{\overrightarrow {Z}}}{\,dz}}+A{\overrightarrow {Z}}={\overrightarrow {b}}} A = { 0 0 0 0 − 1 0 0 0 0 − 1 E J x (z) 0 0 0 0 − 1 0 } {\displaystyle A={\begin{Bmatrix}0&0&0&0\\-1&0&0&0\\0&-\displaystyle {\frac {1}{EJ_{x}(z)}}&0&0\\0&0&-1&0\end{Bmatrix}}}Вектор состояния системы:
Z → = (Q, M, θ, v) T {\displaystyle {\overrightarrow {Z}}=(Q,M,\theta, v)^{T}}Вектор внешней нагрузки:
b → = (q, 0, 0, 0) T {\displaystyle {\overrightarrow {b}}=(q,0,0,0)^{T}}Это дифференциальное уравнение может быть использовано для расчета многоопорных балок с переменным по длине моментом инерции сечения и сложным образом распределенными нагрузками. Для расчета простых балок применяются упрощенные методы. В сопротивлении материалов при расчете статически определимых балок изгибающий момент находится методом сечений. Уравнение
v ″ = M x E J x {\displaystyle v""={\frac {M_{x}}{EJ_{x}}}}интегрируется дважды:
v ′ = θ (z) = ∫ M x (z) E J x d z + C 1 {\displaystyle v"=\theta (z)=\int {\frac {M_{x}(z)}{EJ_{x}}}\,dz+C_{1}} v (z) = ∫ (∫ M x (z) E J x d z) d z + C 1 z + C 2 {\displaystyle v(z)=\int \left(\int {\frac {M_{x}(z)}{EJ_{x}}}\,dz\right)\,dz+C_{1}z+C_{2}}Константы C 1 {\displaystyle C_{1}}, C 2 {\displaystyle C_{2}} находятся из граничных условий, наложенных на балку. Так, для консольной балки, изображенной на рисунке:
M x (z) = − P (L − z) {\displaystyle M_{x}(z)=-P(L-z)} θ (z) = − P L z E J x + P z 2 2 E J x + C 1 {\displaystyle \theta (z)=-PL{\frac {z}{EJ_{x}}}+P{\frac {z^{2}}{2EJ_{x}}}+C_{1}} v (z) = − P L z 2 2 E J x + P z 3 6 E J x + C 1 z + C 2 {\displaystyle v(z)=-PL{\frac {z^{2}}{2EJ_{x}}}+P{\frac {z^{3}}{6EJ_{x}}}+C_{1}z+C_{2}}
Граничные условия:
θ (0) = 0 ⇛ C 1 = 0 {\displaystyle \theta (0)=0\Rrightarrow C_{1}=0} v (0) = 0 ⇛ C 2 = 0 {\displaystyle v(0)=0\Rrightarrow C_{2}=0}Таким образом,
θ (z) = − P L z E J x + P z 2 2 E J x {\displaystyle \theta (z)=-PL{\frac {z}{EJ_{x}}}+P{\frac {z^{2}}{2EJ_{x}}}} v (z) = − P L z 2 2 E J x + P z 3 6 E J x {\displaystyle v(z)=-PL{\frac {z^{2}}{2EJ_{x}}}+P{\frac {z^{3}}{6EJ_{x}}}}Теория изгиба балок Тимошенко
Данная теория базируется на тех же гипотезах, что и классическая, однако гипотеза Бернулли модифицируется: предполагается, что сечения, бывшие до деформации плоскими и нормальными к оси балки, остаются плоскими, но перестают быть нормальными к изогнутой оси. Таким образом, данная теория учитывает деформацию сдвига и касательные напряжения. Учёт касательных напряжений очень важен для расчета композитов и деталей из дерева, так как их разрушение может происходить за счет разрушения связующего при сдвиге.
Основные зависимости:
M = E J d θ d z {\displaystyle M=EJ{\frac {\,d\theta }{\,dz}}} Q = G F α (θ − d v d z) {\displaystyle Q={\frac {GF}{\alpha }}\left(\theta -{\frac {\,dv}{\,dz}}\right)}где G {\displaystyle G} - модуль сдвига материала балки, F {\displaystyle F} - площадь сечения, α {\displaystyle \alpha } - коэффициент, учитывающий неравномерность распределения касательных напряжений по сечению и зависящий от его формы. Величина
γ = θ − d v d z {\displaystyle \gamma =\theta -{\frac {\,dv}{\,dz}}}представляет собой угол сдвига.
Изгиб балок на упругом основании
Данной расчетной схемой моделируются железнодорожные рельсы, а также корабли (в первом приближении).
Упругое основание рассматривается как множество не связанных друг с другом пружинок.
Простейший метод расчета основан на гипотезе Винклера: реакция упругого основания пропорциональна прогибу в точке и направлена навстречу ему:
P = − k ⋅ v {\displaystyle p=-k\cdot v}
где v {\displaystyle v} - прогиб;
P {\displaystyle p} - реакция (на единицу длины балки);
K {\displaystyle k} - коэффициент пропорциональности (называемый коэффициентом постели ).
При этом основание считается двусторонним, то есть реакция возникает как при вдавливании балки в основание, так и при её отрыве от основания. Гипотеза Бернулли сохраняется.
Дифференциальное уравнение изгиба балки на упругом основании имеет вид:
D 2 d z 2 (E J x (z) d 2 v d z 2) + k (z) ⋅ v = q (z) {\displaystyle {\frac {d^{2}}{dz^{2}}}\left(EJ_{x}(z){\frac {d^{2}v}{dz^{2}}}\right)+k(z)\cdot v=q(z)}
где v (z) {\displaystyle v(z)} - прогиб;
E J x (z) {\displaystyle EJ_{x}(z)} - изгибная жесткость (могущая быть переменной по длине);
K (z) {\displaystyle k(z)} - переменный по длине коэффициент постели;
Q (z) {\displaystyle q(z)} - распределенная нагрузка на балку.
При постоянной жесткости и коэффициенте постели уравнение может быть записано в виде:
E J x d 4 v d z 4 + k ⋅ v = q (z) {\displaystyle EJ_{x}{\frac {d^{4}v}{dz^{4}}}+k\cdot v=q(z)}
D 4 v d z 4 + 4 m 4 ⋅ v = q (z) {\displaystyle {\frac {d^{4}v}{dz^{4}}}+4m^{4}\cdot v=q(z)}
где обозначено
4 m 4 = k E J x {\displaystyle 4m^{4}={\frac {k}{EJ_{x}}}}
Изгиб бруса большой кривизны
Для балок, радиус кривизны оси которых ρ 0 {\displaystyle \rho _{0}} соизмерим с высотой сечения h {\displaystyle h}, то есть:
H ρ 0 0, 2 {\displaystyle {\frac {h}{\rho _{0}}}0,2}
распределение напряжений по высоте отклоняется от линейного, а нейтральная линия не совпадает с осью сечения (которая проходит через центр тяжести сечения). Такая расчетная схема используется, например, для расчета звеньев цепей и крюков подъёмных кранов.
Файл:Схема изгиб бруса большой кривизны.png
Поперечное сечение
Формула для распределения напряжений имеет вид:
σ = M F ⋅ e ⋅ y R + y {\displaystyle \sigma ={\frac {M}{F\cdot e}}\cdot {\frac {y}{R+y}}}
где M {\displaystyle M} - изгибающий момент в сечении;
R {\displaystyle R} - радиус нейтральной линии сечения;
F {\displaystyle F} - площадь сечения;
E = R 0 − R {\displaystyle e=R_{0}-R} - эксцентриситет;
Y {\displaystyle y} - координата по высоте сечения, отсчитываемая от нейтральной линии.
Радиус нейтральной линии определяется по формуле:
R = ∫ d F u = ∫ R 1 R 2 b (u) d u u {\displaystyle R=\int {\frac {\,dF}{u}}=\int \limits _{R_{1}}^{R_{2}}{\frac {b(u)\,du}{u}}}
Интеграл берется по площади сечения, координата u {\displaystyle u} отсчитывается от центра кривизны. Справедливы также приближенные формулы:
E = J x R 0 ⋅ F {\displaystyle e={\frac {J_{x}}{R_{0}\cdot F}}}
R 0 = R 0 − J x R 0 ⋅ F {\displaystyle r_{0}=R_{0}-{\frac {J_{x}}{R_{0}\cdot F}}}
Для часто используемых сечений имеются аналитические формулы. Для прямоугольного сечения высотой h {\displaystyle h}:
R = h ln R 0 + h 2 R 0 − h 2 = h ln R 2 R 1 {\displaystyle R={\frac {h}{\ln \displaystyle {\frac {R_{0}+{\frac {h}{2}}}{R_{0}-{\frac {h}{2}}}}}}={\frac {h}{\ln \displaystyle {\frac {R_{2}}{R_{1}}}}}}
где R 1, R 2 {\displaystyle R_{1},R_{2}} - радиусы кривизны внутренней и наружной поверхности балки соответственно.
Для круглого сечения:
R = R 0 + R 0 2 − r 2 2 {\displaystyle R={\frac {R_{0}+{\sqrt {R_{0}^{2}-r^{2}}}}{2}}}
где r {\displaystyle r} - радиус сечения.
Проверка прочности балки
В большинстве случаев прочность балки определяется по максимальным допускаемым напряжениям:
σ m a x < σ T n T {\displaystyle \sigma _{max}<{\frac {\sigma _{T}}{n_{T}}}}где σ T {\displaystyle \sigma _{T}} - предел текучести материала балки, n T {\displaystyle n_{T}} - коэффициент запаса по текучести. В случае хрупких материалов:
σ m a x < σ b n b {\displaystyle \sigma _{max}<{\frac {\sigma _{b}}{n_{b}}}}где σ b {\displaystyle \sigma _{b}} - предел прочности материала балки, n b {\displaystyle n_{b}} - коэффициент запаса по прочности.
U = ∑ i = 1 4 C i K i (α z) {\displaystyle u=\sum _{i=1}^{4}C_{i}K_{i}(\alpha z)}
где функции Крылова:
K 1 (α z) = 1 2 (ch α z + cos α z) {\displaystyle K_{1}(\alpha z)={\frac {1}{2}}(\operatorname {ch} \alpha z+\cos \alpha z)}
K 2 (α z) = 1 2 (sh α z + sin α z) {\displaystyle K_{2}(\alpha z)={\frac {1}{2}}(\operatorname {sh} \alpha z+\sin \alpha z)}
K 3 (α z) = 1 2 (ch α z − cos α z) {\displaystyle K_{3}(\alpha z)={\frac {1}{2}}(\operatorname {ch} \alpha z-\cos \alpha z)}
K 4 (α z) = 1 2 (sh α z − sin α z) {\displaystyle K_{4}(\alpha z)={\frac {1}{2}}(\operatorname {sh} \alpha z-\sin \alpha z)}
а C i {\displaystyle C_{i}} - постоянные.
Функции Крылова связаны зависимостями:
D d z K 1 (α z) = α K 4 (α z) {\displaystyle {\frac {d}{dz}}K_{1}(\alpha z)=\alpha K_{4}(\alpha z)}
D d z K 2 (α z) = α K 1 (α z) {\displaystyle {\frac {d}{dz}}K_{2}(\alpha z)=\alpha K_{1}(\alpha z)}
D d z K 3 (α z) = α K 2 (α z) {\displaystyle {\frac {d}{dz}}K_{3}(\alpha z)=\alpha K_{2}(\alpha z)}
D d z K 4 (α z) = α K 3 (α z) {\displaystyle {\frac {d}{dz}}K_{4}(\alpha z)=\alpha K_{3}(\alpha z)}
Эти зависимости существенно упрощают запись граничных условий для балок:
C 1 = u z = 0; C 2 = 1 α (d u d z) z = 0; C 3 = 1 E J α 2 M z = 0; C 4 = 1 E J α 3 Q z = 0 {\displaystyle C_{1}=u_{z=0};C_{2}={\frac {1}{\alpha }}\left({\frac {du}{dz}}\right)_{z=0};C_{3}={\frac {1}{EJ\alpha ^{2}}}M_{z=0};C_{4}={\frac {1}{EJ\alpha ^{3}}}Q_{z=0}}
На каждом конце балки задаются два граничных условия.
Уравнение собственных колебаний имеет бесконечно много решений. При этом, практический интерес, как правило, представляют только первые несколько из них, соответствующие низшим собственным частотам.
Общая формула для собственной частоты имеет вид:
P k = λ k 2 E J m 0 l 4 {\displaystyle p_{k}=\lambda _{k}^{2}{\sqrt {\frac {EJ}{m_{0}l^{4}}}}}
Для однопролетных балок:
| Закрепление | λ k {\displaystyle \lambda _{k}} | |
|---|---|---|
| Левый конец | Правый конец | |
| Заделка | Заделка | λ 1 = 4, 73; {\displaystyle \lambda _{1}=4,73;} λ 2 = 7, 853; {\displaystyle \lambda _{2}=7,853;} |
| Свободный | Свободный | λ 1 = 0; {\displaystyle \lambda _{1}=0;} λ 2 = 0; {\displaystyle \lambda _{2}=0;} λ k = 2 k + 1 2 π; {\displaystyle \lambda _{k}={\frac {2k+1}{2}}\pi; } |
| Заделка | Шарнирное | λ 1 = 3, 927; {\displaystyle \lambda _{1}=3,927;} λ 2 = 7, 069; {\displaystyle \lambda _{2}=7,069;} λ k = 4 k + 1 4 π; {\displaystyle \lambda _{k}={\frac {4k+1}{4}}\pi; } |
| Шарнирное | Шарнирное | λ k = k 2 π 2 {\displaystyle \lambda _{k}=k^{2}\pi ^{2}} |
| Заделка | Свободный | λ 1 = 1, 875; {\displaystyle \lambda _{1}=1,875;} λ 2 = 4, 694; {\displaystyle \lambda _{2}=4,694;} λ k = 2 k − 1 2 π; {\displaystyle \lambda _{k}={\frac {2k-1}{2}}\pi; } |
Изгиб вид деформации, при котором происходит искривление осей прямых брусьев или изменение кривизны осей кривых брусьев. Изгиб связан с возникновением в поперечных сечениях бруса изгибающих моментов. Прямой изгиб возникает в случае, когда… … Википедия
Изгиб - – деформация детали в направлении перпендикулярном его оси. [Блюм Э. Э. Словарь основных металловедческих терминов. Екатеринбург 2002] Изгиб – деформация, возникающая в балках, плитах перекрытий, ограждающих конструкциях под… … Энциклопедия терминов, определений и пояснений строительных материалов
Бруса, деформированное состояние, возникающее в брусе под действием сил и моментов, перпендикулярных его оси, и сопровождающееся её искривлением (об И. пластинки и оболочки (см. ПЛАСТИНКИ, ОБОЛОЧКА)). Возникающие при И. в поперечном сечении бруса … Физическая энциклопедия
ИЗГИБ, изгиба, муж. 1. Дугообразное искривление, закругленный излом, затейливый поворот. На изгибе реки. Красивый изгиб лебединой шеи. Изгибы дороги. «Их (сосен) корни затейливыми изгибами лежали, как серые мертвые змеи.» Максим Горький. 2. перен … Толковый словарь Ушакова
изгиб - ИЗГИБ, извив, извилина, изворот, излом ИЗВИЛИСТЫЙ, змеистый, изгибистый, излучистый, петлистый … Словарь-тезаурус синонимов русской речи
В сопротивлении материалов вид деформации, характеризующийся искривлением (изменением кривизны) оси или срединной поверхности элемента (балки, плиты и т. п.) под действием внешней нагрузки. Различают изгибы: чистый, поперечный, продольный,… … Большой Энциклопедический словарь
ИЗГИБ, а, муж. Дугообразное искривление. И. реки. Изгибы души (перен.). Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
Напряженное состояние стержня или бруса, сопровождаемое искривлением по сравнению с его первоначальной формой. Различают поперечный И., происходящий под действием нагрузок, направленных в большинстве случаев перпендикулярно оси стержня, и… … Технический железнодорожный словарь
изгиб - Вид деформации тела, выражающийся в изменении его кривизны в одном или нескольких направлениях [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] EN bendingflexure DE Biegung FR flexion … Справочник технического переводчика
ИЗГИБ - вид (см.), при которой ось или срединная поверхность балки, стержня, пластины искривляется под действием внешних сил или температуры. Наибольшее напряжение испытывают наружные слои на выпуклой стороне деформируемого объекта. Деформацией балки при … Большая политехническая энциклопедия
Книги
- Кручение и изгиб тонкостенных авиаконструкций, Уманский А.А. Кручение и изгиб тонкостенных авиаконструкций Воспроизведено в оригинальной авторской орфографии издания 1939 года (издательство "Оборонпром")…
- Продольный изгиб. Кручение, А. Н. Динник. Публикуемые в настоящем томе труды академика А. Н. Динника "Продольный изгиб. Кручение", будучи настольной книгой для инженеров, в настоящее время являются библиографической редкостью. Это…
Деформация изгиба заключается вискривлении оси прямого стержня или визменении начальной кривизны прямогостержня (рис. 6.1). Ознакомимсяс основными понятиями, которые используютсяпри рассмотрении деформации изгиба.
Стержни, работающие на изгиб, называют балками.
Чистым называется изгиб, при которомизгибающий момент является единственнымвнутренним силовым фактором, возникающемв поперечном сечении балки.
Чаще, в поперечном сечении стержнянаряду с изгибающим моментом возникаеттакже и поперечная сила. Такой изгибназывают поперечным.
Плоским (прямым) называют изгиб,когда плоскость действия изгибающегомомента в поперечном сечении проходитчерез одну из главных центральных осейпоперечного сечения.
При косом изгибе плоскость действияизгибающего момента пересекает поперечноесечение балки по линии, не совпадающейни с одной из главных центральных осейпоперечного сечения.
Изучение деформации изгиба начнем сослучая чистого плоского изгиба.
Нормальные напряжения и деформации при чистом изгибе.
Как уже было сказано, при чистом плоскомизгибе в поперечном сечении из шестивнутренних силовых факторов не равеннулю только изгибающий момент (рис. 6.1,в):
Опыты, поставленные на эластичныхмоделях, показывают, что если наповерхность модели нанести сетку линий(рис. 6.1, а), то при чистом изгибе онадеформируется следующим образом(рис. 6.1, б):
а) продольные линииискривляются по длинеокружности;
б) контуры поперечных сечений остаютсяплоскими;
в) линии контуров сечений всюдупересекаются с продольными волокнамипод прямым углом.
На основании этого можно предположить,что при чистом изгибе поперечные сечениябалки остаются плоскими и поворачиваютсятак, что остаются нормальными к изогнутойоси балки (гипотеза плоских сечений приизгибе).
Рис. 6.1
Замеряя длину продольных линий (рис.6.1, б), можно обнаружить, что верхниеволокна при деформации изгиба балкиудлиняются, а нижние укорачиваются.Очевидно, что можно найти такие волокна,длина которых остается неизменной.Совокупность волокон, не меняющих своейдлины при изгибе балки, называется нейтральным слоем (н. с.). Нейтральныйслой пересекает поперечное сечениебалки по прямой, которая называется нейтральной линией (н. л.) сечения.
Для вывода формулы, определяющей величинунормальных напряжений, возникающих впоперечном сечении, рассмотрим участокбалки в деформированном и не деформированномсостоянии (рис. 6.2).
Рис. 6.2
Двумя бесконечно малыми поперечнымисечениями выделим элемент длиной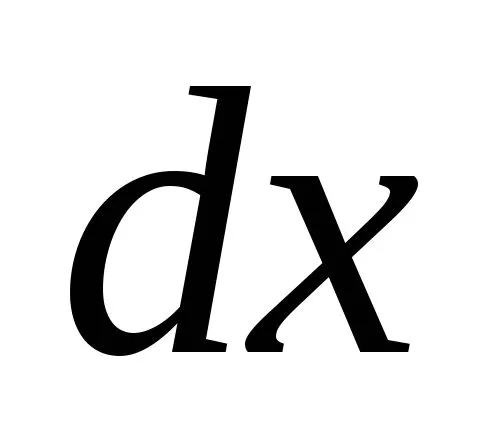 .До деформации сечения, ограничивающиеэлемент
.До деформации сечения, ограничивающиеэлемент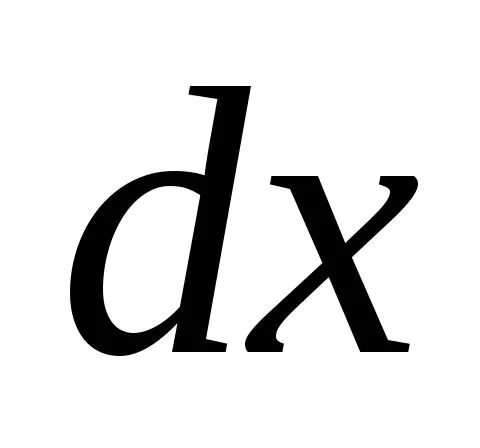 ,были параллельны между собой (рис. 6.2,а), а после деформации они нескольконаклонились, образуя угол
,были параллельны между собой (рис. 6.2,а), а после деформации они нескольконаклонились, образуя угол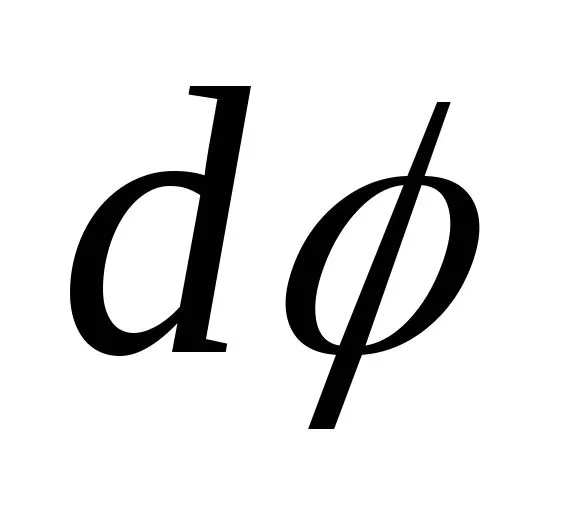 .Длина волокон, лежащих в нейтральномслое, при изгибе не меняется
.Длина волокон, лежащих в нейтральномслое, при изгибе не меняется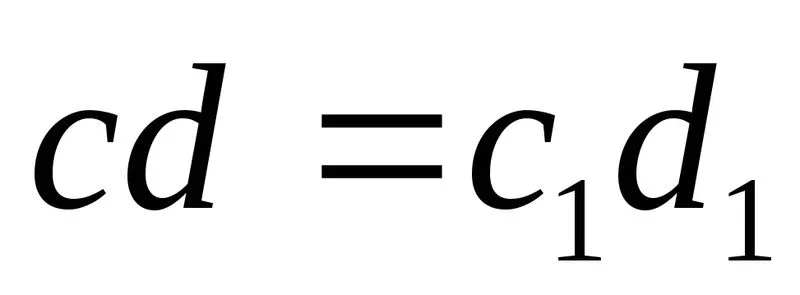 .Обозначим радиус кривизны следанейтрального слоя на плоскости чертежабуквой
.Обозначим радиус кривизны следанейтрального слоя на плоскости чертежабуквой .Определим линейную деформациюпроизвольного волокна
.Определим линейную деформациюпроизвольного волокна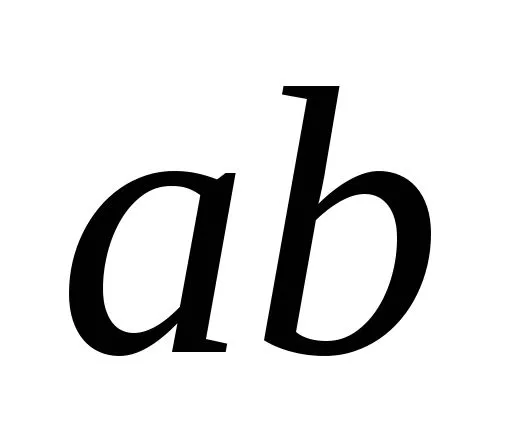 ,отстоящего на расстоянии
,отстоящего на расстоянии от нейтрального слоя.
от нейтрального слоя.
Длина этого волокна после деформации(длина дуги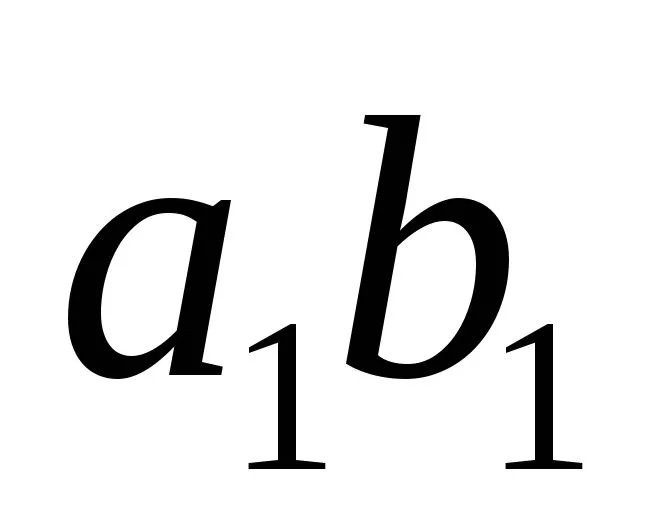 )равна
)равна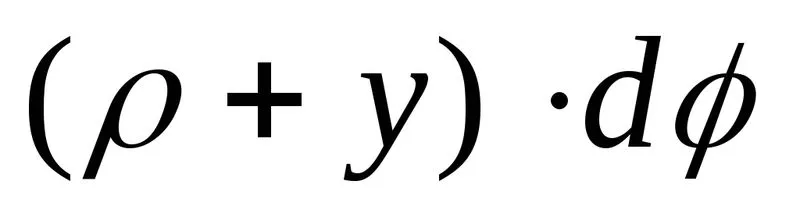 .Учитывая, что до деформации все волокнаимели одинаковую длину
.Учитывая, что до деформации все волокнаимели одинаковую длину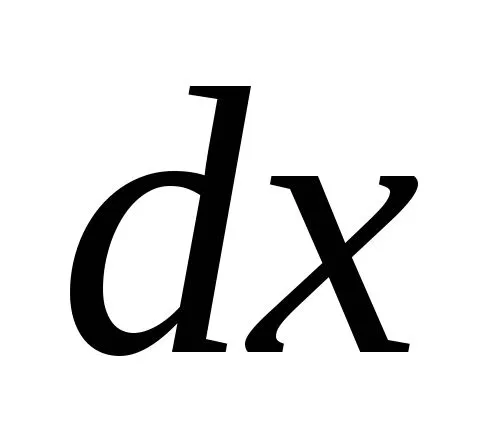 ,получим, что абсолютное удлинениерассматриваемого волокна
,получим, что абсолютное удлинениерассматриваемого волокна
Его относительная деформация
Очевидно, что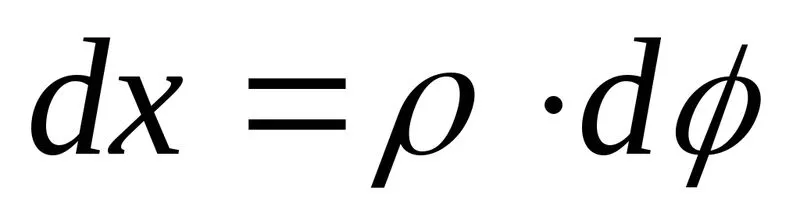 ,так как длина волокна, лежащего внейтральном слое не изменилась. Тогдапосле подстановки
,так как длина волокна, лежащего внейтральном слое не изменилась. Тогдапосле подстановки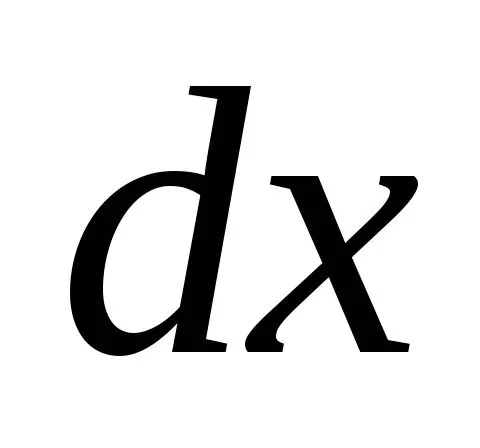 получим
получим
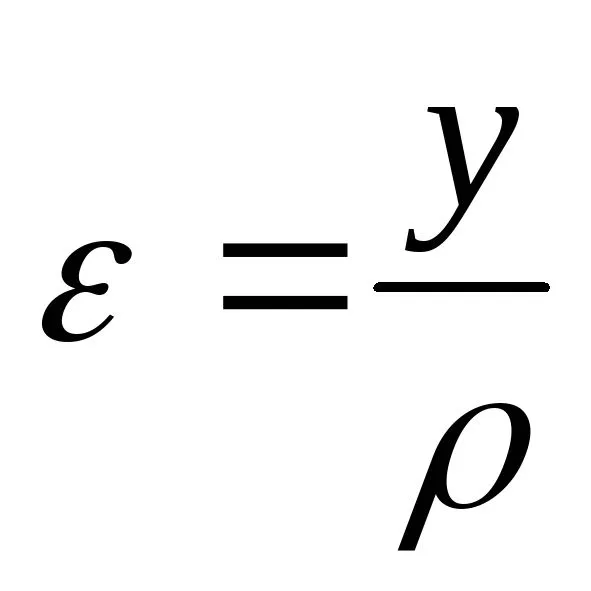 (6.2)
(6.2)
Следовательно, относительная продольнаядеформация пропорциональна расстояниюволокна от нейтральной оси.
Введем предположение, что при изгибепродольные волокна не надавливают другна друга. При таком предположении каждоеволокно деформируется изолировано,испытывая простое растяжение или сжатие,при котором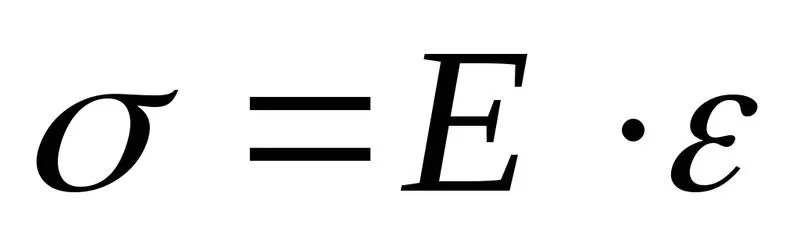 .С учетом (6.2)
.С учетом (6.2)
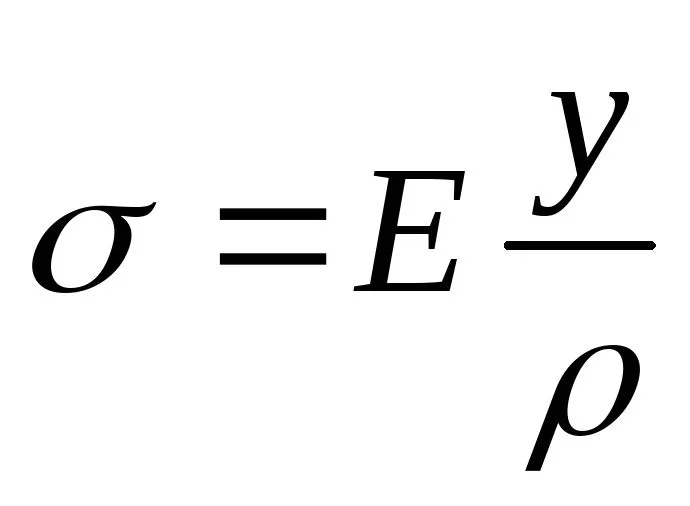 , (6.3)
, (6.3)
т. е. нормальные напряжения прямопропорциональны расстояниям рассматриваемыхточек сечения от нейтральной оси.
Подставим зависимость (6.3) в выражениеизгибающего момента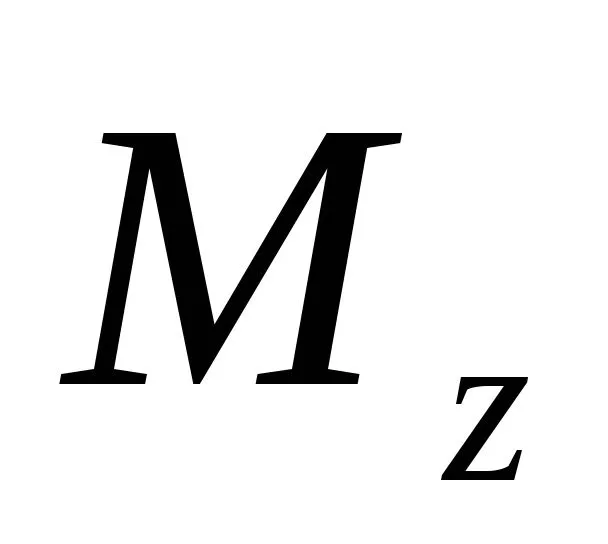 в поперечном сечении (6.1)
в поперечном сечении (6.1)
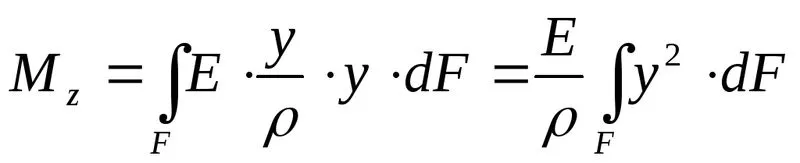 .
.
Вспомним, что интеграл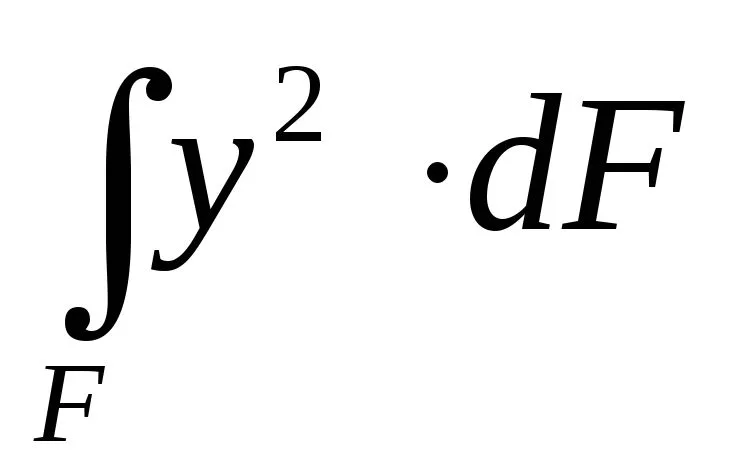 представляет собой момент инерциисечения относительно оси
представляет собой момент инерциисечения относительно оси
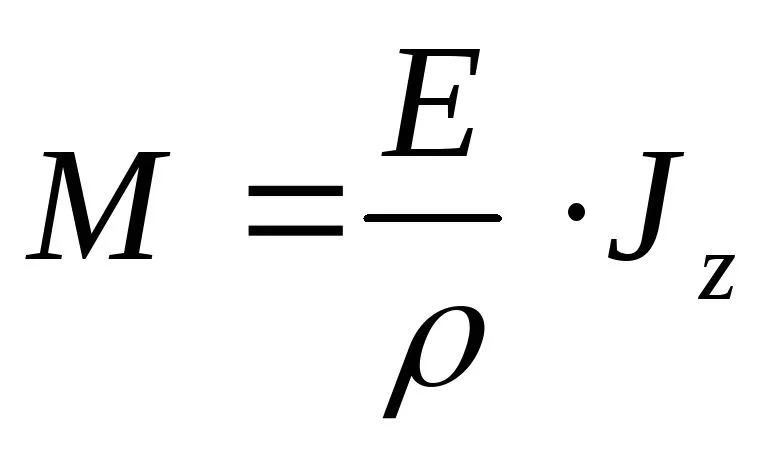 .
.
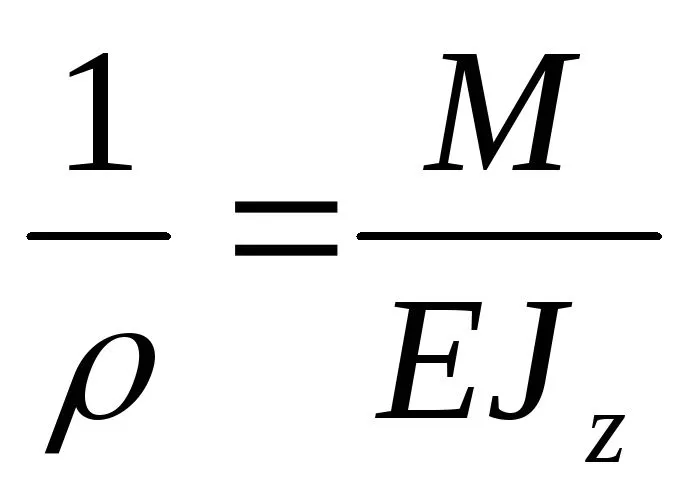 (6.4)
(6.4)
Зависимость (6.4) представляет собойзакон Гука при изгибе, поскольку онасвязывает деформацию (кривизнунейтрального слоя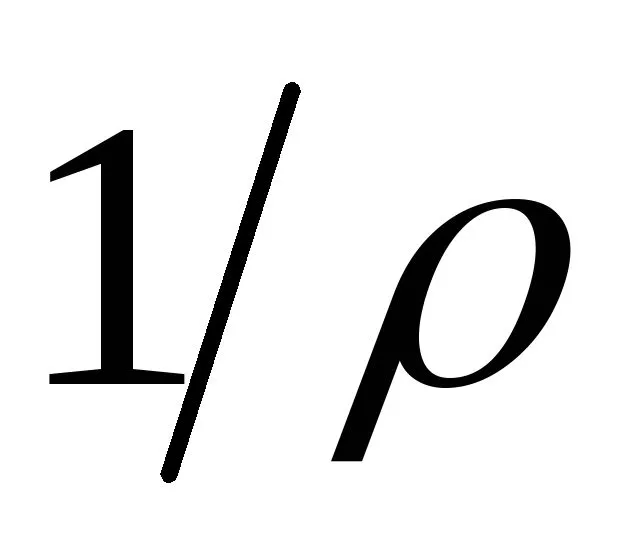 )с действующим в сечении моментом.Произведение
)с действующим в сечении моментом.Произведение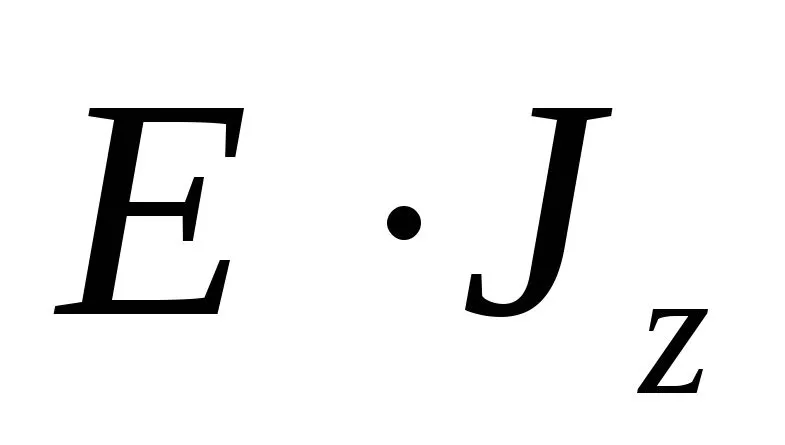 носит название жесткости сечения приизгибе, Н·м 2.
носит название жесткости сечения приизгибе, Н·м 2.
Подставим (6.4) в (6.3)
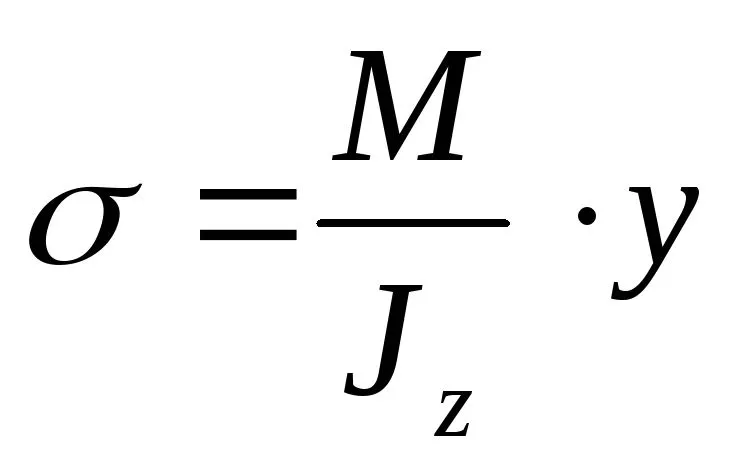 (6.5)
(6.5)
Это и есть искомая формула для определениянормальных напряжений при чистом изгибебалки в любой точке ее сечения.
Для того, чтобы установить,где в поперечном сечении находитсянейтральная линия подставим значениенормальных напряжений в выражениепродольной силы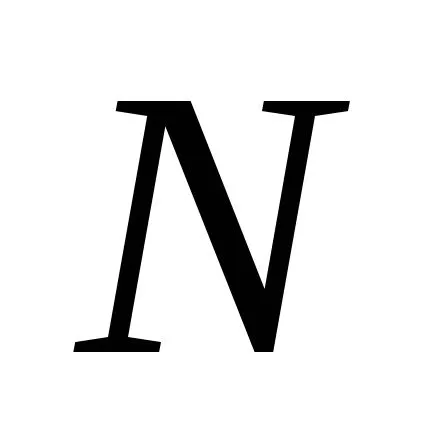 и изгибающего момента
и изгибающего момента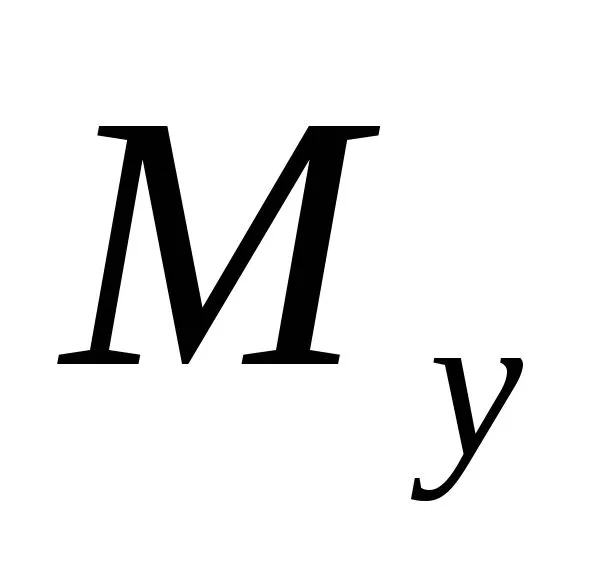
Поскольку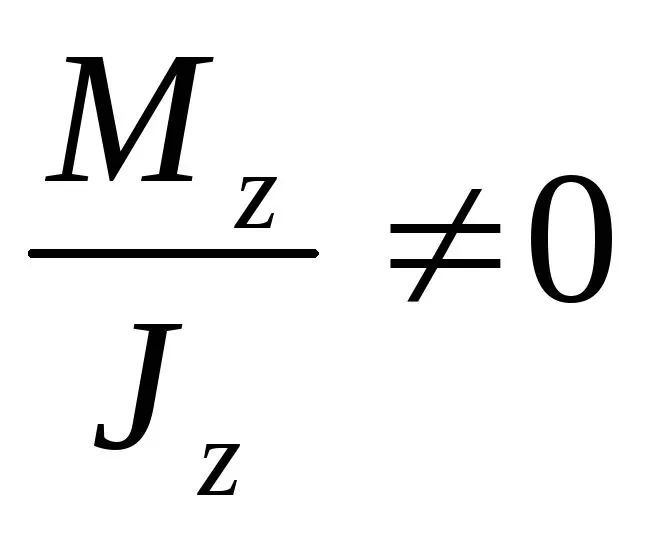 ,
,
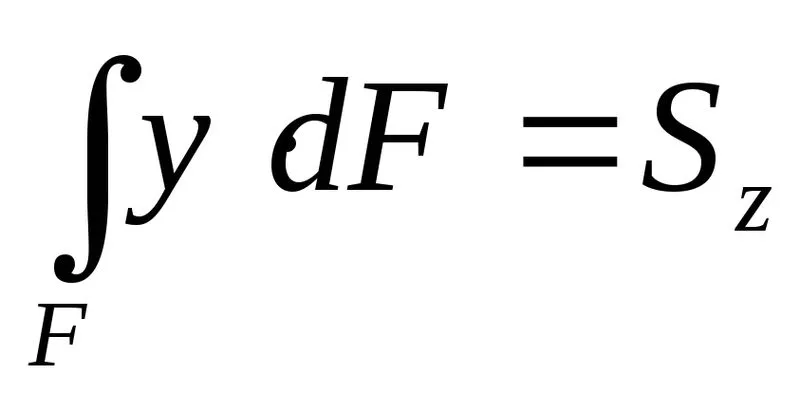 ;
;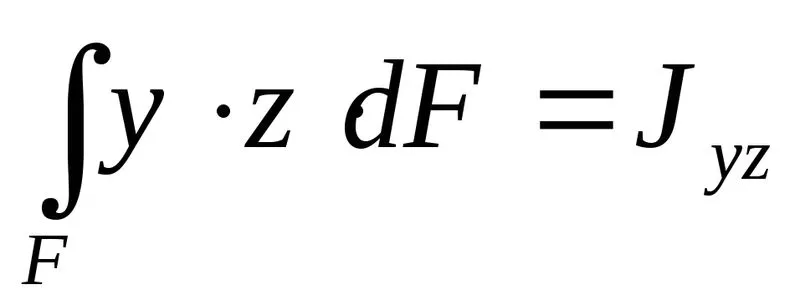
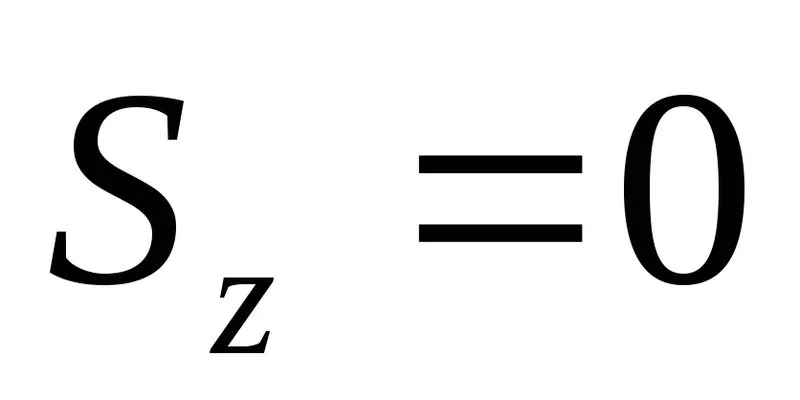 (6.6)
(6.6)
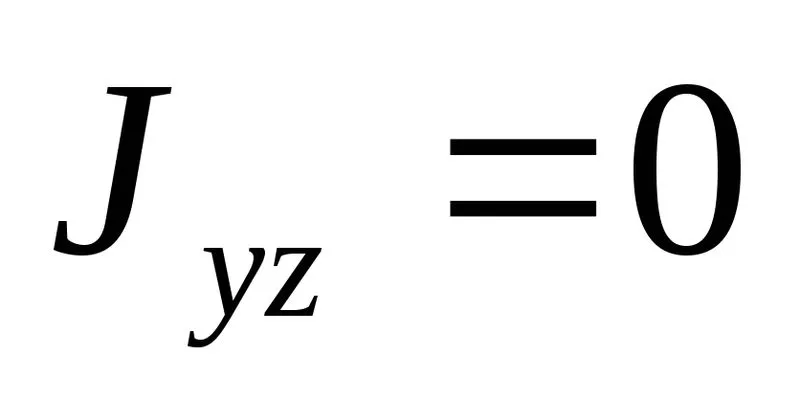 (6.7)
(6.7)
Равенство (6.6) указывает, что ось – нейтральная ось сечения – проходитчерез центр тяжести поперечного сечения.
– нейтральная ось сечения – проходитчерез центр тяжести поперечного сечения.
Равенство (6.7) показывает что и
и - главные центральные оси сечения.
- главные центральные оси сечения.
Согласно (6.5) наибольшей величинынапряжения достигают в волокнах наиболееудаленных от нейтральной линии
Отношение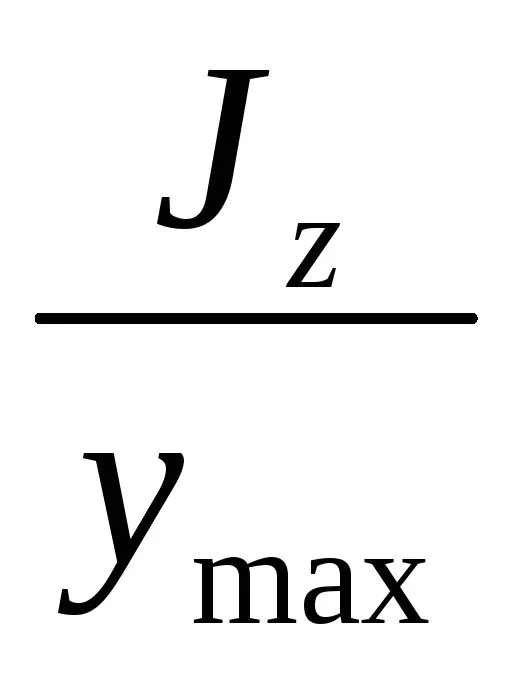 представляет собой осевой моментсопротивления сечения
представляет собой осевой моментсопротивления сечения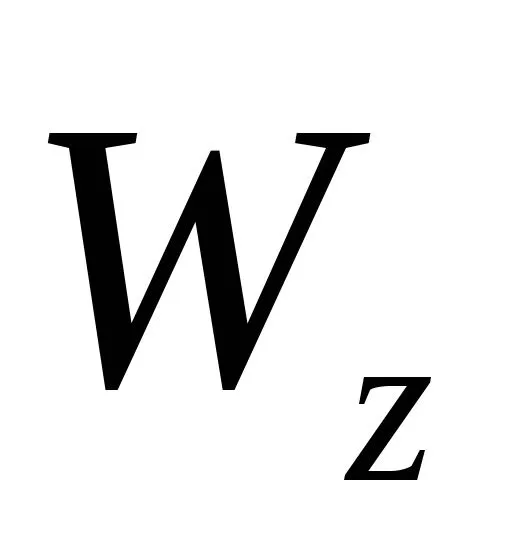 относительно его центральной оси
относительно его центральной оси ,значит
,значит
Значение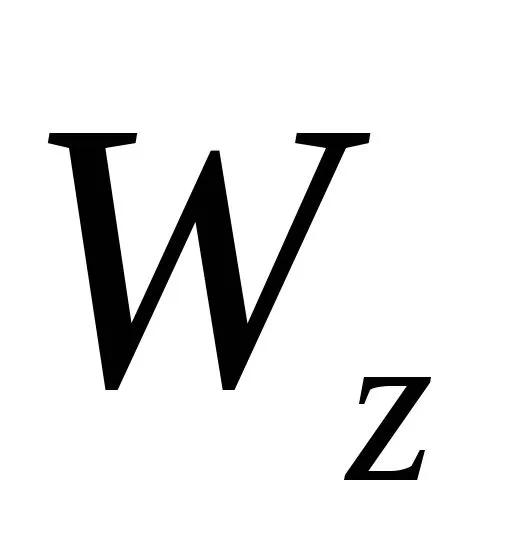 для простейших поперечных сеченийследующее:
для простейших поперечных сеченийследующее:
Для прямоугольного поперечного сечения
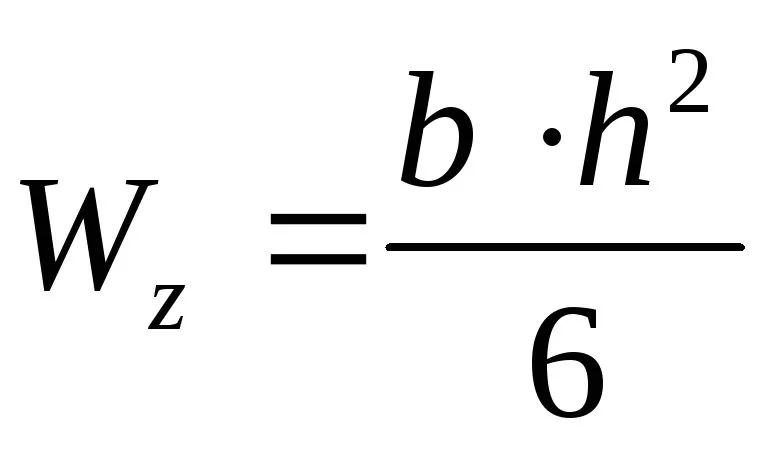 , (6.8)
, (6.8)
где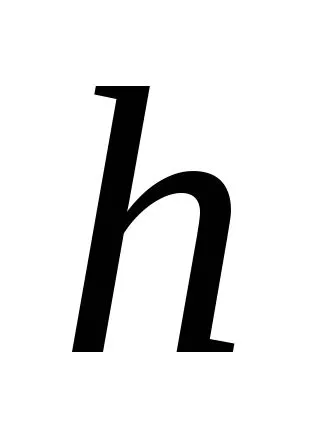 -сторона сечения перпендикулярная оси
-сторона сечения перпендикулярная оси ;
;
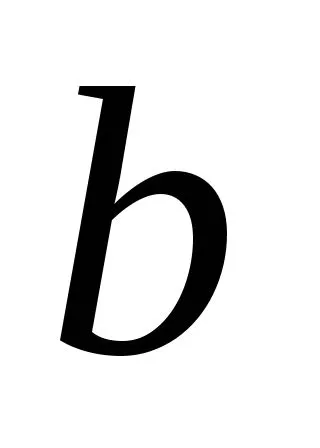 - сторона сечения параллельная оси
- сторона сечения параллельная оси ;
;
Для круглого поперечного сечения
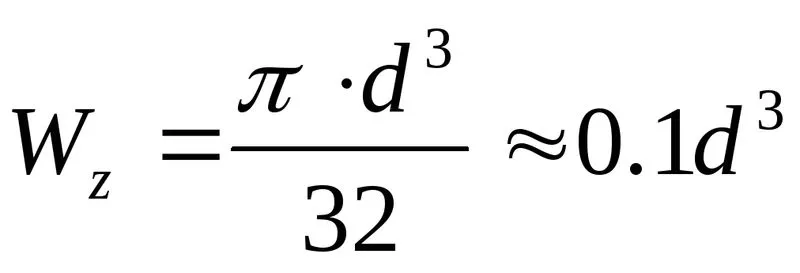 , (6.9)
, (6.9)
где - диаметр круглого поперечногосечения.
- диаметр круглого поперечногосечения.
Условие прочности по нормальнымнапряжениям при изгибе можно записатьв виде
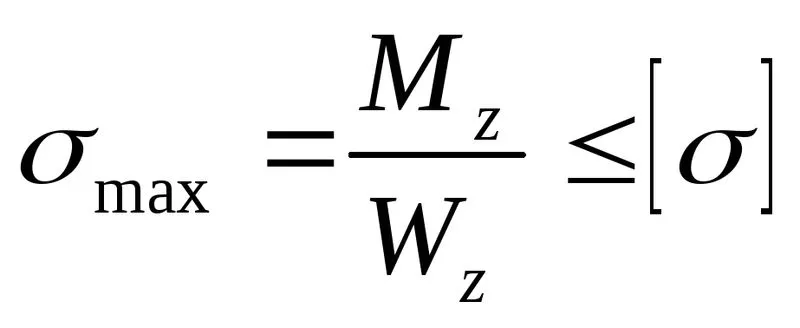 (6.10)
(6.10)
Все полученные формулы получены дляслучая чистого изгиба прямого стержня.Действие же поперечной силы приводитк тому, что гипотезы, положенные в основувыводов, теряют свою силу. Однако практикарасчетов показывает, что и при поперечномизгибе балок и рам, когда в сечении кромеизгибающего момента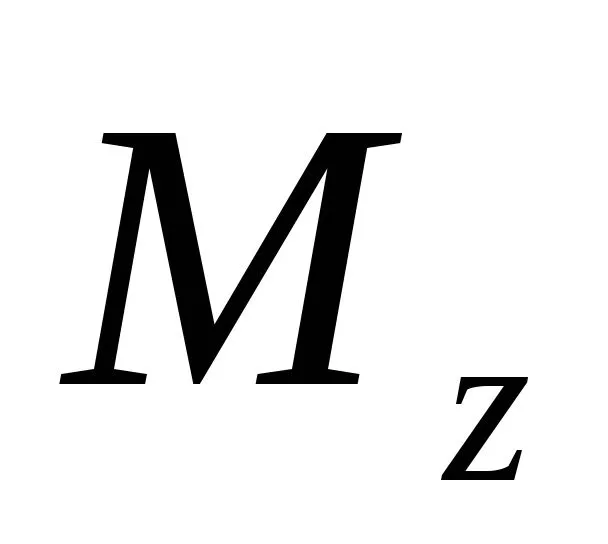 действует еще продольнаясила
действует еще продольнаясила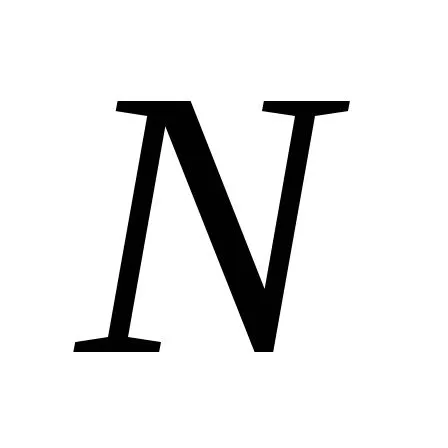 и поперечная сила
и поперечная сила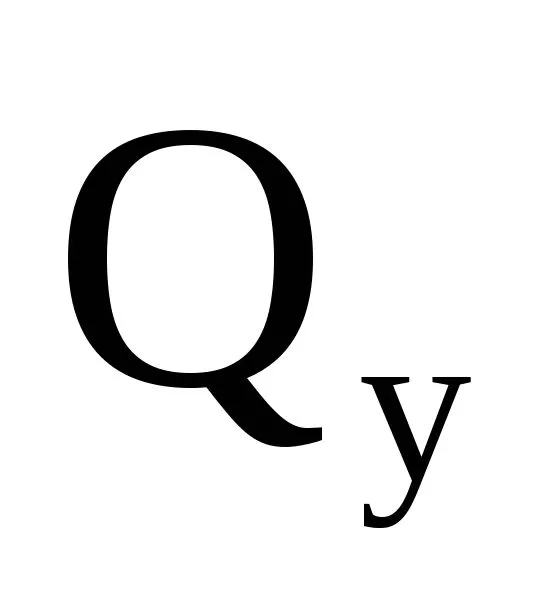 ,можно пользоваться формулами,приведенными для чистого изгиба.Погрешность при этом получаетсянезначительной.
,можно пользоваться формулами,приведенными для чистого изгиба.Погрешность при этом получаетсянезначительной.
изгиб, кривизна реки
Альтернативные описанияИзгиб края седла
Мужское имя (лат. светоносный)
Изгиб реки
Персонаж пьесы ""На дне""
Изгиб морского берега
. "Кривуля" на реке
. "Носок" конского седла
Выступ седла
Герой пьесы "На дне"
Герой, "На дне"
Гнутый выступ седла
Дугообразный поворот реки
Евангелист
Ж. изгиб, погиб, кривизна, излучина; заворот реки, дуга; низменный и травный или лесистый мыс; поемный луг, огибаемый рекою. Иногда лука принимается, обратно, в значении залива, затона, заводи или это новорос. травная лощина, луг. Седельных лук две, передняя и задняя. Мотри, возгрей к луке не примерзни! дразнят неженку. Церк. лукавство, кривизна души. Лука реки, как и колено, локоть, иногда говорят вместо плесо, т. е. не изгиб, а прямое русло меж изгибов. Лука реки (дуга), лукно, лукошко (гнутое, гнуток), лук (гнутый, т. е. мечущий стрелы), лукать и пр. общего корня. Лук м. лучок, согнутая в дугу полоса; упругая полоса, деревянная, роговая, стальная, напрягаемая тетивою, для пусканья стрел. Лучок с прикладом, самострел; лучок с двойною тетивою, для метанья глиняных пуль, казарга. Лучок токарный, сверлильный, род смычка, коим вертят снаряды взад и вперед. Лучок пилы, железный станочек для нее. Лучок рыболовный, кармак, уда на белорыбицу. Шерстобитный лук или лучок, трехаршинный шест с кобылкою и тетивою, которою пушат, бьют шерсть, ударяя по ней катеринкою, колотушкой. Дуга, дужка, пол-обруча, гнуток, напр. на кибитке. Лучок на косе, крюк, грабок, грабки, грабли для косьбы хлеба. Сеть для ловли певчих пташек (тайник перекидывается на двух палочках, лучок на пол-обруче). Прибор в запряжке коноводных лошадей. Новг. отдельное место для путников, на лодке-тихвинке, под крышей, настланной по дугам. конного солдата ноги лучком. Кому до чего, а стрелку до лука. Тугой лук, то сердечный друг. Лук, что царь, стрелы, что посланники. Лук добро и к бою, и во щах (игра слов). Плуг кормит, а лук (оружие) портит, стар. о мужике, солдате. Из лука не мы, из пищали не мы, а попить, поплясать, против нас не сыскать! Невелик лук, да туг. Как из лука стрела. Будто с лука спрянул. Оба луки, оба туги. Лук, стар. мера земли; на сев. две обжи,
Загиб реки
Изгиб морского берега
Изгиб реки
Изгиб реки или седла
Изгиб русла
Изгиб седла
Излучина реки
Имя итальянского художника Синьорелли
Имя какого библейского персонажа переводится с латинского как "свет"
Коллега Матфея по евангелие
Коллега Матфея, Марка и Иоанна
Крутая извилина русла реки с близко сходящимися у перешейка концами
Крутой изгиб реки
Кто из евангелистов изображается в виде тельца
Миротворец в пьесе "На дне"
Морской изгиб
Мужское имя
Мужское имя, рифмующееся с букой
Мужское имя: (латинское) светоносный
Один из евангелистов
Персонаж "На дне"
Поворот реки
Поворот седла
Речное искривление
Русский мореход, открывший морской проход из Северной Двины в Северную Норвегию (XIV в.)
Самарская на Волге
Спутник апостола Павла
Хорошее имя для русского мужика
Часть седла
Главный миротворец в пьесе Горького "На дне"
Персонаж пьесы Горького "На дне"
Странник в пьесе "На дне"
Выступающий изгиб переднего или заднего края седла
Утешитель
Мудищев
Персонаж пьесы А. П. Чехова "Медведь"
Персонаж произведения Ж. Мольера "Лекарь поневоле"
Грек из евангелистов
Речной изгиб
Изгиб речного русла
Изгиб побережья
Излучина седла
Загогулина седла
Гнутый бортик седла
Имя Хлопова в "Ревизоре"
Изогнутый выступ седла
Чем не имя для русского мужика
Русское мужское имя
Мужское имя, рифмующееся с мукой
Подходящ. русскому парню имя
Дугообразный изгиб реки